Equidistribution in number theory
Mathematics Colloquium
Date
Wednesday, February 11, 2026 15:30 - 16:30
Speaker
Valentin Blomer (University of Bonn)
Location
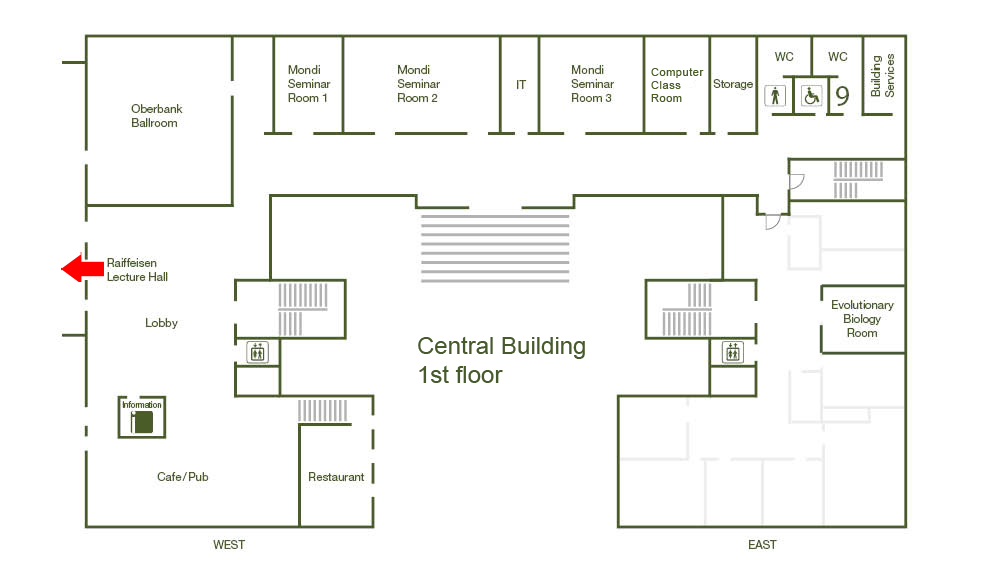
Raiffeisen Lecture Hall, Central Building
Series
Colloquium
Tags
Mathematics Colloquium
Host
Laszlo Erdös, Uli Wagner
Contact
Arithmetically interesting objects are often a small set in some larger ambient space and one may ask how they are distributed. In this talk, we take a geometric perspective and consider subsets of the modular curve, i.e. the upper complex half plane modulo SL(2, Z), a space with a rich structure. I will present various classical and modern equidistribution problems and describe what tools can be used to establish equidistribution results.