Disjointness in Ergodic and Number Theory
Mathematics Colloquium
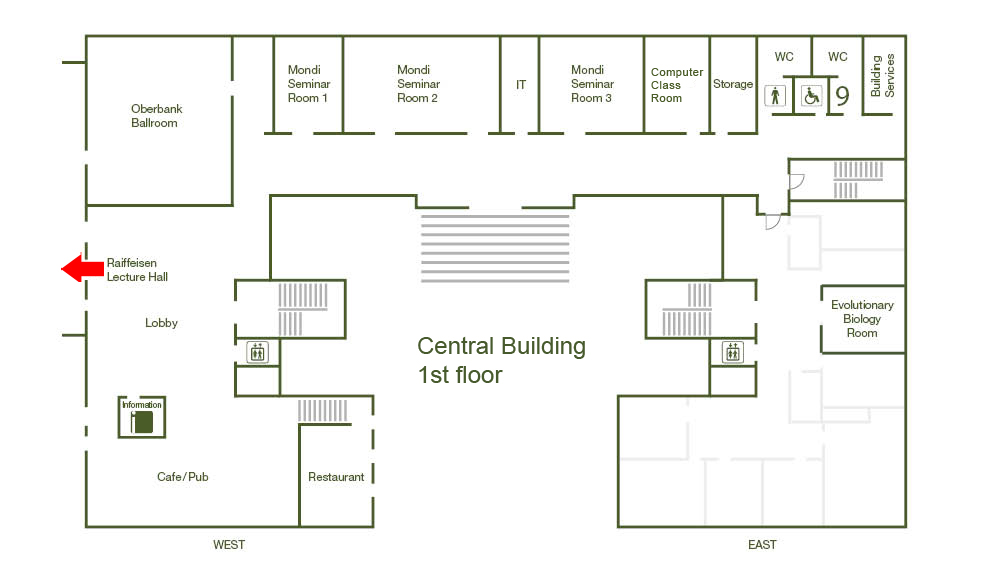
Furstenberg introduced in 1967 joinings and disjointness as fundamental tools for studying structural properties of measure preserving systems. We will review some old and some new results in this direction that classify joinings or even establish disjointness. In particular we will discuss how these can be used for number theoretical ‘joint equidistribution' problems. For instance disjointness results can be used to describe the joint equidistribution of low lying rational points on closed horocycles related by different powers, the joint equidistribution of rational points on spheres and the shape of the lattice in the orthogonal complement, or other refinements of Duke’s theorem concerning the equidistribution of CM-points on the modular surface.
The talk will be based on various joint works with M. Akka, E. Lindenstrauss, M. Luethi, Ph. Michel, U. Shapira, A. Wieser