On volume preserving almost Anosov flows
Date
Monday, February 28, 2022 15:30 - 16:30
Speaker
Henk Bruin (Faculty of Mathematics, University of Vienna)
Location
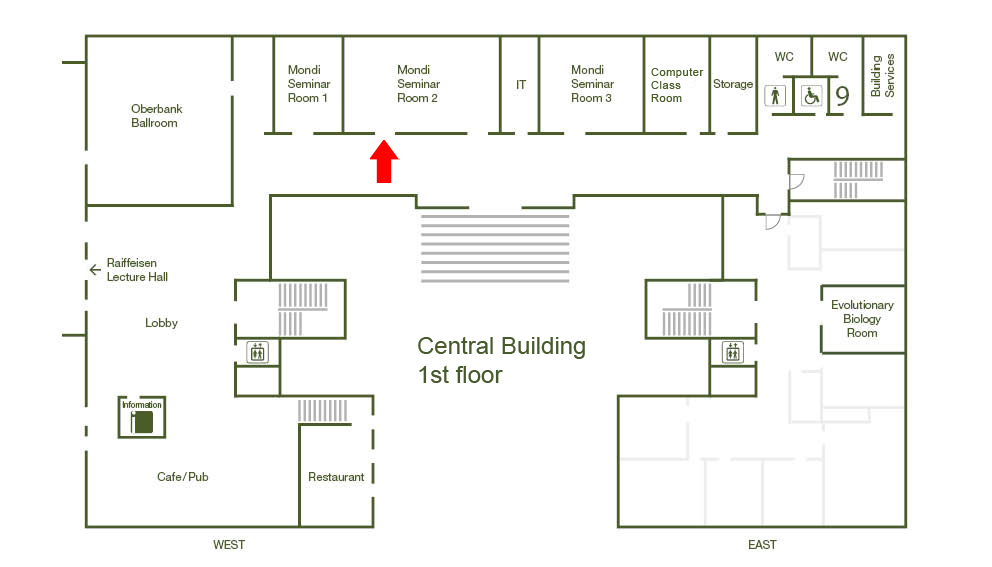
IST Austria, Mondi 2
Series
Seminar/Talk
Tags
DynamIST, mathematical_seminar_ics
Host
Vadim Kaloshin
Contact
IST Austria / Kaloshin Group
Url
We call a flow on a compact manifold "almost Anosov'' if the Anosov property of being hyperbolic everywhere is violated at (a finite collection of) periodic solutions. In this talk, I will present results on what happens if the flow (on a 3-manifold) preserves volume and has a periodic orbit of neutral saddle type. Asymptotics of the resulting intermittent behaviour can be accurate estimated and give rise to (non-standard) Central Limit Theorem or Stable Laws for such flows.